The Curse of Dimensionality.

When you were born, a lot of things quickly became axioms. You always accelerate downward at $1g$, the sun shines from above, the pressure is $1 \text{atm}$. We've gotten so used to this that it's terrifying to go on a roller coaster; we shine flashlights onto the bottom of our faces while telling horror stories; our ears have to do significant adjustment to the $0.78\:\text{atm}$ experienced on airplanes. However, one fundamental axiom restricts us forever—and no matter how hard we try, we have no chance of escaping it (outside our powerful imagination). This principle of the universe is that we live in three spatial dimensions.

In many ways, this is a blessing. Imagine the complexity of kinematics calculations if projectiles flew through 10-dimensional space^[1][2][3][4]. However, in a ten-dimensional world, we'd have a much lower chance of getting into the San Francisco housing crisis. Most importantly, three dimensions are easy to understand, and work quite well for everything we know. However, our intuition fails miserably as the number of dimensions increases, which jeopardizes our ability to solve mathematical problems, discover new cures to diseases, and begs the crucial question of what goes wrong in higher dimensions?

Consider the following simple construction in $\mathbb{R}^2$: we take a $2 \times 2$ square, centered at the origin. Place a quarter-circle in each of the corners, and finally, inscribe a circle centered at the origin tangent to all four quarter-circles, as shown^[5]:

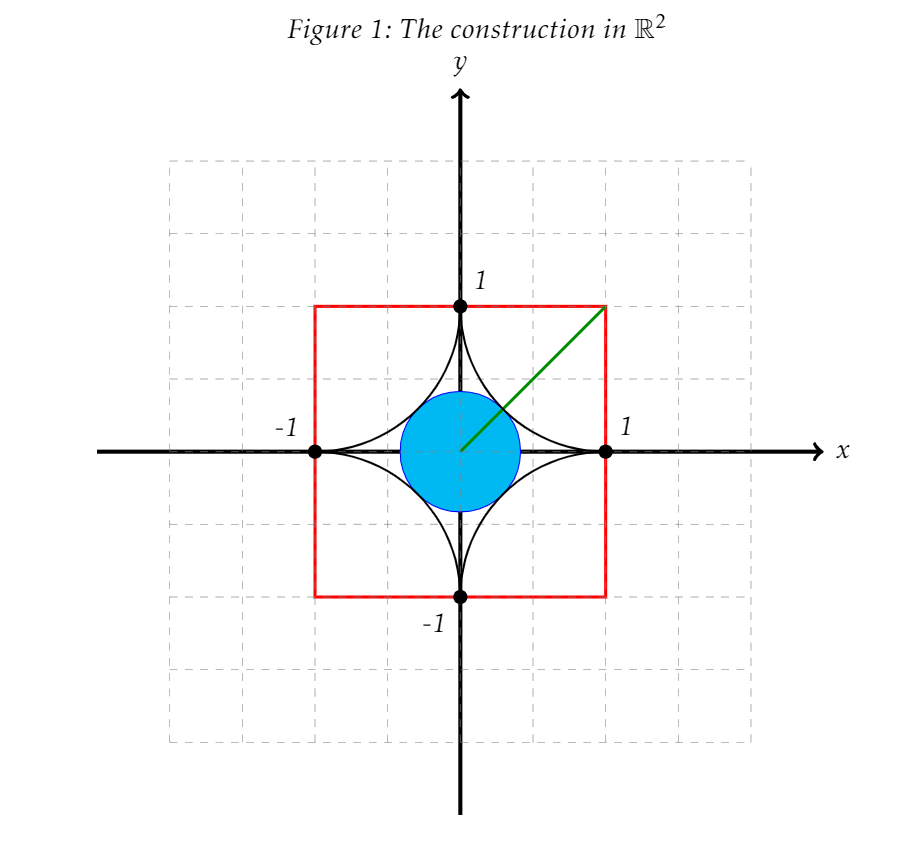
Let's find the ratio $q_{2}$ of the area of the inner circle to the area of the bounding box. Using some sick geometry, we get that the radius of the inner circle is $\sqrt{2}-1$, and thus its area is $S_{c}=\pi(\sqrt{2}-1)^2$. Therefore, we get $$q_{2} = \frac{\pi(\sqrt{2}-1)^2}{2^2} \approx 0.135$$ Now consider the analog in $\mathbb{R}^{3}$. Instead of a square, take a $2\times2\times2$ cube, centered at the origin. In each corner, inscribe one-eighth of a sphere. Now, inscribe an inner sphere, centered at the origin, tangent to all eight pieces. What is $q_{3}$? Well, the radius of the inner sphere is $\sqrt{3}-1$. Using the volume formula for a 2-sphere, we get $$q_{3} = \frac{\frac{4}{3}\pi(\sqrt{3}-1)^3}{2^3} \approx 0.205$$ What does this ratio, $q_{d}$, approach, as the number of dimensions increases? That is, what is the value of $$\lim_{d \to \infty} q_{d}\:\text{ ?}$$ You may think, intuitively, that this ratio approaches 1. After all, it makes sense that the sphere gets larger and larger, and in infinite dimensions, begins to take up most of the space in the bounding box. Those of you who have had more exposure to higher-dimensional geometry may say that the ratio approaches zero^[6]. Some starry-eyed mathematicians may hope that it approaches one-half. In fact, $$\lim_{d \to \infty} q_{d} = \infty$$ If you're familiar with multivariable calculus, you can use $d$-dimensional spherical coordinates to derive the closed form\margintext{The gamma in the denominator is the Euler Gamma function, an extension of the factorial. To see where this comes from, try deriving this equation (Exercise) and look at the collected terms from the nested integrals.} $$q_{d} = \frac{\pi^{\frac{d}{2}}(\sqrt{d}-1)^{d}}{\Gamma(\frac{d}{2}+1)2^{d}}$$ and see the limit for yourself^[7].

How does this make any sense? Well, the first place our intuition fails us is by the idea of the "bounding box". In fact, this box is not "bounding" at all---rather, it's a pretty arbitrary construction that the inner sphere can easily leave. In fact, consider the 4-dimensional case. The radius of the inner 3-sphere is $\sqrt{4}-1=1$. So, in four dimensions, our inner sphere starts pushing up against the boundary of the box! In higher dimensions, the result is even more striking. Observe that $$q_{7} = \frac{\frac{16}{105}\pi^3(\sqrt{7}-1)^7}{2^7} \approx 1.21$$ So at this point, the volume of the inscribed sphere is straight up larger than that of the bounding box. Here's the question: where is all this extra area concentrated? Obviously, the most volume the ball can fit in the bounding box has an upper bound of $2^n$. The extra area must all be concentrated in the small protrusions the ball makes out of the bounding box---in $\mathbb{R}^7$, this is a mere 17\% of the volume, but as the dimensionality increases, closer and closer to 100\% of the volume of the $d$-ball is concentrated on the surface. This is a fundamental tenet of the curse of dimensionality: In higher dimensions, almost all of the volume of a ball is concentrated arbitratily close to its surface. Another way of seeing this is, given $V_{d}(r)$ is the volume of a $d$-ball with radius $r$, it is true that for any $\epsilon > 0$, $$\lim_{d \to \infty}\frac{V_{d}(r)}{V_{d}(r - \epsilon)} = \infty$$ This leads to the following famous joke: $$\textit{Never buy an orange in high dimensions. Once you peel it, there's nothing left!}$$